non_coder = N - coder
xs = [...Array(N).keys()];
ys = xs.map(x => cost_prog(non_coder, x, c_0))
Plot.lineY(ys).plot({
height: 400, width: 450, grid: true,
y: { label: "↑ c(n,p)", domain:[0,1] },
x: { label: "p/n →" }
})Algebraic model
Model Sketch
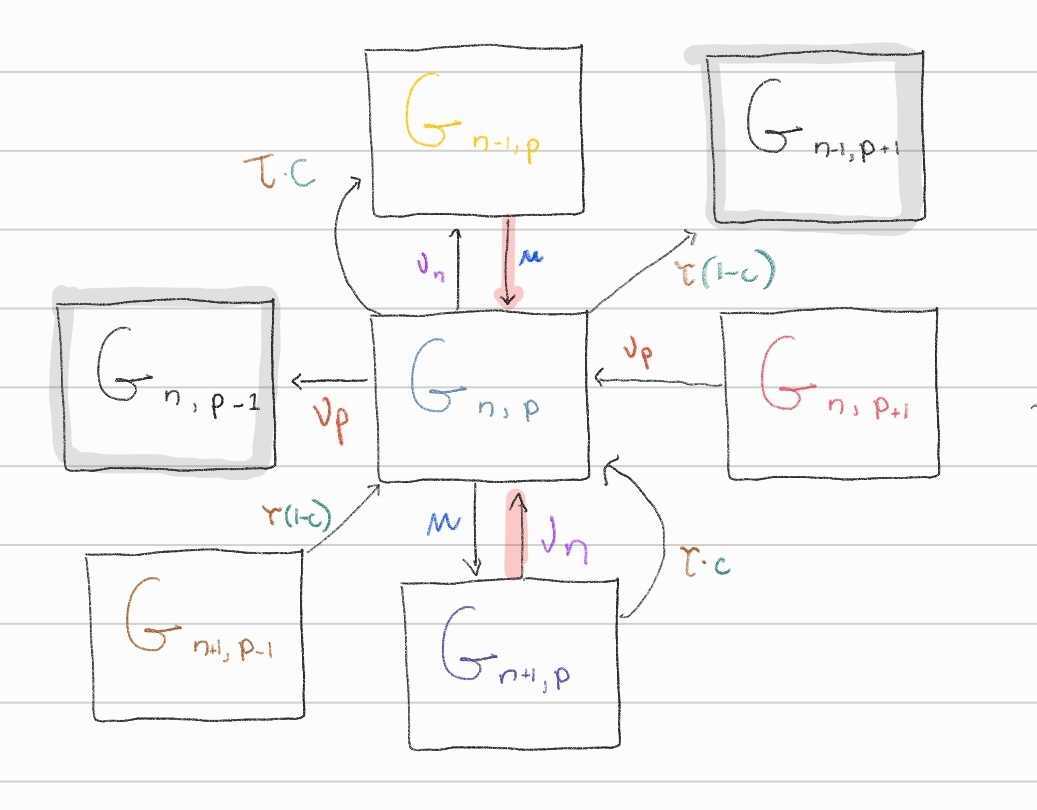
There are research groups \(G\) with a number of non-programmers \(n\) and programmers \(p\). In a data-driven world, we assume that learning to code confer a large benefit to programmers over non-programmer such that \(\alpha << \beta\). There is a constant rate of influx of students who do not know how to learn to code in research groups \(\mu\). There is a cost of learning to code \(c(p,n)\), which depend on the number of programmers and non-programmers within group. We assume that programmers and non-programmers have different graduation rates, \(\nu_p\) and \(\nu_n\), with \(\nu_p > \nu_n\).
We model the group life cycle with the following master equation:
\[\begin{align*} \frac{d}{dt}G_{n,p} &= \mu(G_{n-1,p} - G_{n,p}) + \nu_n \Big((n+1)G_{n+1,p}-nG_{n,p}\Big) \\ &+ \Big[ \tau_g(n+1,p-1)(1-c(n+1, p-1)G_{n+1,p-1} - \tau_g(n,p)G_{n,p} \Big] \\ &+ \nu_p\Big((p+1)G_{n,p+1} - pG_{n,p} \Big) \\ &+ \tau_g(n+1,p)(1-c(n+1,p))G_{n+1,p} \end{align*}\]
Learning to code confers a collective benefits on individuals \(\tau_g(n,p; \alpha, \beta) \propto \frac{\bar{Z}_{n,p}}{Z_{n,p}}\), where
\[\log(Z_{n,p}) \sim \alpha * n + \beta * p\] \[\log(\bar{Z}_{n,p}) \sim \alpha (n-1) +\beta (c * p + (1-c)(p+1))\]
We can think of \(\bar{Z}_{n,p}\) as the potential benefits over \(Z_{n,p}\). Reorganizing the terms, we get:
\[\begin{align*} \log[\tau_g(n,p; \alpha, \beta))] &= \alpha (n-1) +\beta (c * p + (1-c)(p+1)) - \alpha * n + \beta * p \\ &= -\alpha + \beta(1-c) \end{align*}\]
Note that \(\tau_g\) ends up being a function of \(n, p\) through the cost function: \[c(n,p) = c_0*e^{-\frac{p}{n}}\]
You can explore both functions below:
Cost function
\(p/n\) \(\Rightarrow\) / =
\(c(n,p)\) = (c=1 means that non-coders always fail to learn to code; c=0 means non-coders always succeed)
Non-programmers can still learn to code when \(p=0\) because of \(c_0\)
I woudl expect a bigger difference when we go from no prorammers in the team to one programmer
\(p/n\) \(\Rightarrow\) / =
\(c(n,p)\) = (c=1 means that non-coders always fail to learn to code; c=0 means non-coders always succeed)
Non-programmers can still learn to code when \(p=0\) because of \(c_0\)
I woudl expect a bigger difference when we go from no prorammers in the team to one programmer
Group benefits
\(p/n\) \(\Rightarrow\) / =
Julia model
Initialization scheme
function initialize_u0(;N::Int=20)
N += 1 # add column for zeroth case
G = zeros(N, N)
for i=1:N, j=1:N
G[i,j] = 1/(N*N)
end
return ArrayPartition(Tuple([G[n,:] for n=1:N]))
end
μ = 0.001 # inflow new students-non coders
νₙ = 0.01 # death rate non-coders
νₚ = 0.05 # death rate coders
α = 0.01 # benefits non coders
β = 0.1 # benefits coders
p = [μ, νₙ, νₚ, α, β]
n = 9
u₀ = initialize_u0(N=n)
tspan = (0., 1000.)c(n, i) = 0.95 * exp(-i / n) # cost function
τ(n, i, α, β) = exp(-α + β*(1 - c(n, i))) # group benefits
function life_cycle_research_groups!(du, u, p, t)
G, N, P = u, length(u.x), length(first(u₀.x)) # Note that there can be no coders but not non-coders
μ, νₙ, νₚ, α, β = p
for n=1:N, i=1:P
println("n:$(n), i:$(i), G.x[n][i]:$(G.x[n][i])")
coder, non_coder = i-1, n-1 # we distinguish indices from actual values.
du.x[n][i] = 0
non_coder > 0 && ( du.x[n][i] += μ*(G.x[n-1][i]) ) # 1st term
# for everybody
# println("2: $(νₙ*non_coder*G.x[n][i])")
du.x[n][i] -= νₙ*non_coder*G.x[n][i]
# println("3: $(νₚ*coder*G.x[n][i])")
du.x[n][i] -= νₚ*coder*G.x[n][i]
# upper boxes don't exist
if i < P
# non_coder > 0 && println("4: $(τ(non_coder, coder, α, β)*G.x[n][i] )")
# We don't want to pass non_coder = 0 to τ()
non_coder > 0 && ( du.x[n][i] -= τ(non_coder, coder, α, β)*G.x[n][i] ) # 4th term
# println("5: $(νₚ*(coder+1)*G.x[n][i+1])")
du.x[n][i] += νₚ*(coder+1)*G.x[n][i+1] # 5th term
end
# the bottom boxes don't exist
if n < N
# println("6: $(μ*G.x[n][i])")
du.x[n][i] -= μ*G.x[n][i] # 1st term
du.x[n][i] += τ(non_coder+1, coder, α, β)*(c(non_coder+1, coder))*G.x[n+1][i] # 6th term
du.x[n][i] += νₙ*(non_coder+1)*G.x[n+1][i] # 2nd term
coder > 0 && ( du.x[n][i] += τ(non_coder+1, coder-1, α, β)*(1-c(non_coder+1, coder-1))*G.x[n+1][i-1] ) # 3rd term
end
end
end